Как математики вычислили меридиан Земли

Земля круглая – об этом известно даже не одну тысячу лет. Древние греки строго это доказывали и не оставляли попыток измерить меридиан Земли.
Первый кому это удалось сделать с наибольшей точностью был греческий математик Эратосфен (276-194 до н.э.). Длина окружности Земли ему была нужна прежде всего для того, чтобы составить первый атлас об известной и исследованной ее части. И судить о размерах нашей планеты он мог, зная только точные данные.

Эратосфен Киренский (около 276-194 до н. э)

Получить он их смог следующим образом. В то время, всем было известно, что в городе Сиена (Асуан) один день в году, в полдень, Солнце находится точно в зените, т.е. на максимальной высоте над горизонтом. Всего на несколько минут 22 июня в этом городе исчезает тень от вертикального шеста, а также полностью освещается дно колодца. Таким образом, солнечный луч в Сиене (N) перпендикулярен поверхности Земли и проходит через ее центр – точку Z. Эратосфен, живший в Александрии (точка А), ровно в полдень измерил длину тени от вертикального шеста. В результате у него получился треугольник АВС (АС – шест, АВ – тень). Прямая СZ пересекает параллельные прямые СВ и NZ и, по свойству параллельных прямых, углы $ABC$ и $AZN$ равны как накрест лежащие ( $\angle ABC=\angle AZN=\alpha$ ).

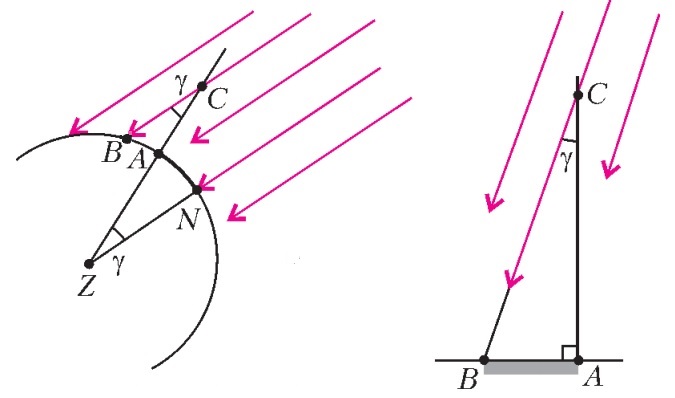
Длина дуги AN есть расстояние между Александрией и Сиеной. Воспользуемся формулой вычисления длины дуги при известных вписанном угле, который на нее опирается, и длине окружности: $x=\frac{L}{360^\circ} \cdot \alpha$ , $L$ — длина окружности Земли, $x$ — длина дуги AN. Расстояние между городами Эратосфену было известно – примерно 800 км. Угол $\alpha$ он вычислил из треугольника АВС и получил 7,2°. Подставляем данные и получаем, что длина окружности Земли (т.е. длина ее меридиана) 40000 км.

На материале статьи В. Протасова «Геометрия звездного неба» («Квант», №2, 2010, с. 14-22)

Добавить комментарий Отменить ответ